Class 9 Polynomials Practice Paper – Questions with Solutions

Polynomials

79 Views 0 Comment January 3, 2026

Section A (1 × 6 = 6 marks)

(Multiple Choice Questions)

Which of the following is a polynomial?
$(a) $\dfrac{1}{x} + 3$ \quad (b) $\sqrt{x} + 2$ \quad (c) $4x^2 - 3x + 7$ \quad (d) $x^{-2} + 1$$
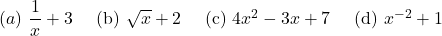
A polynomial of degree 4 has at most
(a) 3 terms
(b) 4 terms
(c) 5 terms
(d) 6 terms
$\text{The coefficient of } x^3 \text{ in } 5x^3 - 2x^2 + x - 9 \text{ is}$
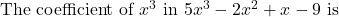
(a) 2
(b) 5
(c) –2
(d) 1
Which of the following is a monomial?
$(a) $x^2 + 1$ \quad (b) $3x^2y$ \quad (c) $x - y$ \quad (d) $x^2 + y^2\quad$
$\text{The degree of the polynomial } 7x^5 - 4x^2 + 9 \text{ is}$

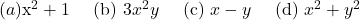
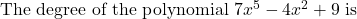
(a) 2
(b) 5
(c) 7
(d) 9
Which expression is a binomial?
$(a) $x$ \quad (b) $x^2 + 3x + 1$ \quad (c) $2x^3$ \quad (d) $x + 5$\quad$

Section B (2 × 4 = 8 marks)

Find the value of k if is a factor of

$4x^3 - 3x^2 + kx - 6$

Factorise:

$x^3 - 27$

Without actually calculating the cubes, find the value of:

$(10)^3 + (5)^3 + (-15)^3$

Find the remainder when

$f(x) = 2x^3 + x^2 - 5x + 7$

is divided by $x - 1$ .

Section C (3 × 3 = 9 marks)

Using factor theorem, factorise:

$x^2 - 7x + 10$

Without actual division, show that

$3x^3 - 5x^2 - 2x + 4$

is divisible by

Using suitable identity, expand:

$\left(\frac{3}{2}x - \frac{1}{3}\right)^2$

Section D (5 × 1 = 5 marks)

If

$x^2 + ax + b = (x + 3)(x - 5)$

find the values of a and b, and hence factorise:

$x^2 + ax - b$

Answer Key

Section A – MCQs

$1.\ (c)\ 4x^2 - 3x + 7$

$2.\ (c)\ 5\ terms$

$3.\ (b)\ 5$

$4.\ (b)\ 3x^2y$

$5.\ (b)\ 5$

$6.\ (d)\ x + 5$

Section B

7. Find the value of

$Given,\ f(x)=4x^3 - 3x^2 + kx - 6$

$Since\ (x+2)\ is\ a\ factor,\ f(-2)=0$

$4(-2)^3 - 3(-2)^2 + k(-2) - 6 = 0$

$-32 - 12 - 2k - 6 = 0$

$-50 - 2k = 0$

$k = -25$

8. Factorise

$x^3 - 27$

$x^3 - 27 = (x - 3)(x^2 + 3x + 9)$

9. Without calculating cubes

$(10)^3 + (5)^3 + (-15)^3$

$a^3 + b^3 + c^3 - 3abc = (a+b+c)(a^2 + b^2 + c^2 - ab - bc - ca)$

$Here,\ a+b+c = 10 + 5 - 15 = 0$

$\therefore\ value = 0$

10. Remainder theorem

$f(x) = 2x^3 + x^2 - 5x + 7$

$Remainder = f(1)$

$= 2(1)^3 + (1)^2 - 5(1) + 7$

$= 2 + 1 - 5 + 7 = 5$

Section C

11. Factorise using factor theorem

$x^2 - 7x + 10$

$= (x - 5)(x - 2)$

12. Prove divisibility

$f(x) = 3x^3 - 5x^2 - 2x + 4$

$f(1) = 3 - 5 - 2 + 4 = 0$

$\therefore\ (x - 1)\ is\ a\ factor$

13. Expand

$\left(\frac{3}{2}x - \frac{1}{3}\right)^2$

$= \left(\frac{3}{2}x\right)^2 - 2\left(\frac{3}{2}x\right)\left(\frac{1}{3}\right) + \left(\frac{1}{3}\right)^2$

$= \frac{9}{4}x^2 - x + \frac{1}{9}$

Section D

14. Find and

$x^2 + ax + b = (x + 3)(x - 5)$

$= x^2 - 2x - 15$

$a = -2,\ b = -15$

$x^2 + ax - b = x^2 - 2x + 15$

Leave A Comment Cancel reply

error: Content is protected !!