Number System Class 9 Worksheet - Extra Questions for Exams

48 Views 0 Comment January 3, 2026

Before attempting the worksheet, watch this complete tutorial on the Number System for Class 9. It will help you understand concepts clearly and solve questions confidently.

👉 Watch first. Practice next. Score better!
Complete Number System tutorial for Class 9 below ⬇️

Section A: Multiple Choice Questions

(1 × 10 = 10 Marks)

$\textbf{1. The decimal expansion of } \boldsymbol{\frac{7}{125}} \textbf{ is:}$

$\textbf{(a)}\ \text{terminating}$

$\textbf{(b)}\ \text{non-terminating repeating}$

$\textbf{(c)}\ \text{non-terminating non-repeating}$

$\textbf{(d)}\ \text{irrational}$

2. Which of the following is an irrational number?

$(a) $\sqrt{49}$ \quad (b) $\dfrac{22}{7}$ \quad (c) $\sqrt{5}$ \quad (d) $0.375$$

$\text{3. The value of } 0.999\ldots \text{ is:} \\ \text{(a) } 0.9 \\ \text{(b) } 1 \\ \text{(c) } \frac{9}{10} \text{(d) } 0$

4. The product of a rational number and an irrational number is always

(a) rational
(b) integer
(c) irrational
(d) whole number

5. Which of the following has a terminating decimal expansion?

$(a)\ 3\frac{3}{7}$

$(b)\ 5\frac{5}{8}$

$(c)\ 11\frac{11}{15}$

$(d)\ 7\frac{7}{12}$

6. The square root of 0.09 is

(a) 0.9
(b) 0.03
(c) 0.3
(d) 3

7. How many rational numbers lie between 2 and 3?

(a) 1
(b) 10
(c) 100
(d) infinitely many

$\textbf{8. } \sqrt{12} \times \sqrt{3}$

$\textbf{(a)}\ 6 \\[6pt] \textbf{(b)}\ \sqrt{36} \\[6pt] \textbf{(c)}\ 12 \\[6pt] \textbf{(d)}\ \sqrt{15}$

9. Which number is NOT a whole number?

(a) 0
(b) 1
(c) –1
(d) 5

10. The decimal expansion of an irrational number is

(a) terminating
(b) repeating
(c) non-terminating non-repeating
(d) non-terminating repeating

Section B: Very Short Answer Questions

(2 × 10 = 20 Marks)

11. $\text{Find three rational numbers between } 2\frac{2}{5} \text{ and } 3\frac{3}{5}.$

12. $\text{Express } 0.125 \text{ in the form } \frac{p}{q}.$

13. $\text{Is } \sqrt{18} \text{ a rational number? Justify your answer.}$

14. Find the value of

$\sqrt{49} + \sqrt{16} - \sqrt{9}$

15. Write whether the following are rational or irrational:

$(i)\ \sqrt{7} (ii)\ 0.4 (iii)\ \frac{5}{11}$

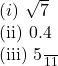
16. $\text{Find the value of } (3 + 2\sqrt{5})^2.$

17. Write any two irrational numbers between 3 and 4.

$\textbf{18. } \text{Simplify: } \sqrt{50} - \sqrt{8}$

$\textbf{19. } \text{If } a = \sqrt{3} \text{ and } b = \sqrt{12}, \text{ find } ab.$

$\textbf{20. } \text{State whether } 0 \text{ is a natural number. Give reason.}$

Section C: Short Answer Questions

(3 × 10 = 30 Marks)

$\text{21. Find five rational numbers between } \frac{1}{3} \text{ and } \frac{2}{3}.$

$\textbf{22. }\ \text{Represent } \sqrt{6} \text{ on the number line using geometrical construction.} \textbf{23. }\ \text{Prove that } \sqrt{5} \text{ is an irrational number.}$