Class 10 Maths Number System Solved Practice Paper

Section A – 1 Mark Each (4 × 1 = 4)

Q1. State whether the decimal expansion of is terminating or non-terminating.
(Similar to CBSE 2019)

Q2. Write the HCF of two consecutive natural numbers.
(Similar to CBSE 2020)

Q3. Is the number $0.375$ a rational number? Give reason.
(Similar to CBSE 2022)

Q4. Write the prime factorisation of 90.
(Similar to CBSE 2021)

---

Section B – 2 Marks Each (4 × 2 = 8)

Q5. Find the LCM of 24 and 36 using prime factorisation method.
(Similar to CBSE 2019)

Q6. Check whether ​ has a terminating decimal expansion or not.
(Similar to CBSE 2024)

Q7. Find the HCF of 135 and 225 using Euclid’s Division Algorithm.
(Repeated: CBSE 2024)

Q8. Express ​ in decimal form.
(Similar to CBSE 2023)

---

Section C – 3 Marks Each (2 × 3 = 6)

Q9. Use Euclid’s Division Algorithm to find the HCF of 867 and 255.
(Repeated: CBSE 2024)

Q10. Find the largest positive integer that divides 398 and 436 leaving remainders 7 and 11 respectively.
(Similar to CBSE 2024)

---

Section D – 4 Marks (1 × 4 = 4)

Q11. Prove that is irrational.
(Repeated: CBSE 2024, similar in 2022 & 2020)

Check solution and answer of each question in the video!

 

 

 

Some Additional Practice Questions for Practice

A. 1 Mark Questions

1. Write the decimal expansion of

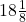
2. State whether 0.1010010001… is a rational or irrational number.

3. Write the HCF of 1 and any prime number.
4. Is the number 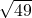a rational number? Give reason.

B. 2 Marks Questions

5. Find the LCM of 18 and 30 using prime factorisation.
6. Check whether the decimal expansion of 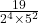is terminating or non-terminating.

7. Express 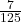in decimal form.

C. 3 Marks Questions

8. Use Euclid’s Division Algorithm to find the HCF of 455 and 42.
9. Find the largest number that divides 615 and 963 leaving remainder 6 in each case.
10. Find the HCF and LCM of 24 and 90 and verify that:

D. 4 Marks Questions

11. Prove that 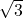is irrational.

12. Prove that 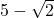is irrational.